惠州市岚方实业有限公司
电话:400-6296-898
传真:0752-2042189
邮箱:sales@lanfsy.com
地址:惠州市博罗县罗阳镇西北路8号
邮编:516100
滤波器在嵌入式开发中的设计
什么是滤波器?
各种传感器信号通过一些噪声信号和过滤器可以更好地降低和去除噪声,恢复一个真正有用的信号。滤波器是从特定范围去除或“过滤”频率分量的电路。也就是说,它将信号的频谱分离为要通过的频率分量和要阻塞的频率分量。如果您对频域分析没有太多经验,您可能仍然不确定这些频率分量是什么,以及它们如何在一个不能同时具有多个电压值的信号中共存。让我们看一个简单的例子来帮助澄清这个概念。假设您有一个由完美的5 kHz 正弦波组成的音频信号。我们知道正弦波在时域中的样子,而在频域中,我们只能看到5 kHz 的频率“尖峰”。现在假设您激活了一个500 kHz 振荡器以将高频噪声引入您的音频信号。您在示波器上看到的信号仍然是一系列电压,每个时刻都有数值,但信号看起来会有所不同,因为时域变化现在必须反映5kHz 正弦波和高频噪声波动。然而,在频域中,正弦波和噪声是同时存在于信号中的独立频率分量。正弦波和噪声占据信号频域表示的不同部分。换句话说,您可以通过在低频发送信号并阻止高频来滤除噪声。下图是正弦波和噪声信号频域不同部分的分布示意图。
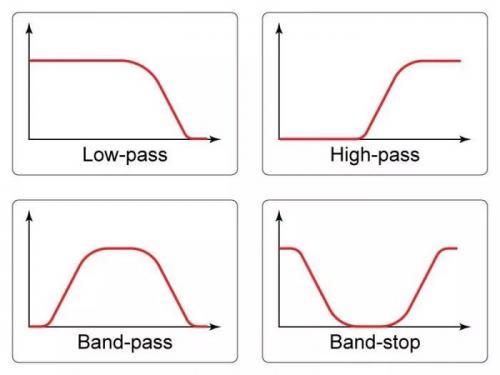
根据滤波器频率响应的一般特性,滤波器可以分为几大类。当滤波器通过低频而阻挡高频时,称为低通滤波器,当阻挡低频而通过高频时,称为高通滤波器。还有一些带通滤波器只通过相对较窄的频率范围,而带阻滤波器只阻止相对较窄的频率范围。每个滤波器的频域表示如下图所示。
滤波器也可以根据用于实现电路的组件类型进行分类。无源滤波器使用电阻、电容和电感,由于这些元件没有放大能力,无源滤波器只能保持或降低输入信号的幅度。另一方面,有源滤波器包含有源元件,例如晶体管或运算放大器,如下图所示,因此它们可以过滤信号并应用增益。

RC低通滤波器
要创建无源低通滤波器,必须将电阻元件和电抗元件组合在一起。换句话说,您需要一个由电阻器和电容器或电感器组成的电路。理论上,电阻-电感(RL) 低通拓扑在滤波能力方面与电阻-电容(RC) 低通拓扑相似。然而,在实践中,电阻电容方法更为常见,因此本文的其余部分将重点介绍RC 低通滤波器。 RC 低通滤波器的示意图如下所示。

RC 低通响应可以通过在信号路径上串联一个电阻器和一个与负载并联的电容器来产生。在图中,负载是单个组件,但在实际电路中它可能更复杂,例如用于测量滤波器响应的模数转换器、放大器或示波器的输入级。认识到电阻器和电容器构成了与频率相关的分压器,我们可以直观地分析RC 低通拓扑的滤波行为。重新绘制RC 低通滤波器,使其看起来像一个分压器,如下所示。

当输入信号的频率较低时,电容的阻抗与电阻的阻抗相比相对较高,因此大部分输入电压会在电容两端(以及负载两端,与电容并联)下降。在高输入频率下,电容器的阻抗与电阻器的阻抗相比变得更低,从而降低了电阻器两端的电压并降低了传递给负载的电压。因此,低频通过而高频被阻挡。尽管对RC 低通函数的这种定性解释是重要的第一步,但当您真正需要设计电路时,它并不是很有用,因为术语“高频”和“低频”非常模糊。工程师必须创建通过和阻止某些频率的电路。例如,在上面的音频系统中,我们希望保留5 kHz 信号并拒绝500 kHz 信号。这意味着您需要一个在5 kHz 和500 kHz 之间从通过切换到截止的滤波器。
RC滤波器截止频率滤波器不引起显着衰减的频率范围称为通带,滤波器不引起显着衰减的频率范围称为阻带。模拟滤波器,例如RC 低通滤波器,总是从通带逐渐过渡到阻带。这意味着滤波器无法识别信号停止通过并开始阻塞信号的频率。然而,工程师需要一种方便而简洁的方法来总结滤波器的频率响应,其中截止频率概念发挥了作用。如果您查看RC 滤波器的频率响应图,您会发现术语“截止频率”不是很准确。信号频谱被“分割”成图像的两个部分,其中一个被保留,另一个被丢弃。它不适用,因为随着频率从截止点以下移动到截止点以上,衰减会逐渐增加。 RC 低通滤波器的截止频率实际上是输入信号幅度降低3 dB 的频率(选择该值是因为幅度降低3 dB 对应于功率降低50%)。所以截止频率也被称为-3dB频率,实际上是一个更准确和信息量更大的名称。术语带宽是指滤波器的通带宽度,对于低通滤波器,带宽等于-3dB 频率,如下图所示。
滤波器响应可视化
评估滤波器对信号的影响最方便的方法是检查滤波器的频率响应图。通常称为波特图,该图在垂直轴上绘制幅度(以分贝为单位),在水平轴上绘制频率。在100 Hz、100 Hz 和1 kHz 之间,这种配置允许在很宽的频率范围内快速准确地评估滤波器的行为。下图是频率响应图的示例。如果输入信号的幅度为1 V,并且频率等于水平轴上的相应值,则曲线上的每个点代表输出信号的幅度。例如,当输入频率为1 MHz 时,输出幅度(假设输入幅度为1 V)将为0.1 V(因为-20 dB 对应于10 倍的衰减系数)。您花在滤波器电路上的时间越多,该频率响应曲线的一般形状就会变得非常熟悉。通带曲线几乎完全平坦,并且随着输入频率接近截止频率而开始下降得更快。最终,衰减变化率(称为滚降)稳定在20 dB/十年。也就是说,输入频率每增加10 倍,输出信号的幅度就会降低20 dB。
评估低通滤波器性能如果您仔细绘制本文前面设计的滤波器的频率响应,您会发现在5kHz 时幅度响应基本上为0dB(即几乎为零衰减),而在500kHz 时幅度响应可以。大约-14 dB(对应于0.2 的增益)。这些值与上一节中进行的计算一致。因为RC 滤波器总是从pass 到stop 逐渐过渡,衰减永远不会达到无穷大,所以不可能设计一个“完美”的滤波器,即完全去除噪声而不影响正弦波的滤波器。相反,我们总是不得不做出妥协。将截止频率移近5 kHz 会导致更多的噪声衰减,但也会更多地衰减您想要发送到扬声器的正弦波。将截止频率移近500 kHz 会降低正弦频率的衰减,但也会降低噪声频率的衰减。早些时候,我们讨论了滤波器如何修改信号中各种频率分量的幅度。然而,除了幅度效应之外,电抗电路元件总是会引入相移。

低通滤波器相移相位的概念描述了一个周期信号在其周期中特定时刻的值。因此,当我们说电路引起相移时,我们的意思是输入信号和输出信号之间存在偏差。输入和输出信号不再同时开始和结束循环。 45或90等相移值表示产生的偏差量。电路中的每个电抗元件都会引入90 相移,但这种相移不会同时发生。输出信号的相位与输出信号的幅度一样,随着输入频率的增加而逐渐变化。由于RC 低通滤波器具有电抗元件(电容器),因此原理图最终会引入90 相移。与幅度响应一样,相位响应最容易通过检查水平轴表示对数频率的图表来评估。以下描述代表一般模式。有关更多详细信息,请参见下图。相移最初为0,然后逐渐增加,直到在截止频率处相移达到45,并且在这部分响应中变化率逐渐增加截止频率后,相移继续增加,但变化率随相位变化而增大逐渐减小,变化率在接近90时变得非常小,实线为幅度响应,虚线为相位响应。截止频率为100 kHz。截止频率处的相移为45。
二阶低通滤波器到目前为止,我们假设RC低通滤波器由一个电阻和一个电容组成。此配置是一阶滤波器。无源滤波器的“阶”由电路中电抗元件(即电容器或电感器)的数量决定。高阶滤波器具有更多的无功分量,从而导致更多的相移和更陡峭的滚降,后者是增加滤波器阶数的主要动机。例如,将电抗元件添加到一阶到二阶或二阶到三阶滤波器会使最大滚降增加20 dB/decade。
次级滤波器围绕由电感器和电容器组成的谐振电路构建,这种拓扑通常称为电阻-电感-电容(RLC)。但是,也可以创建二阶RC 滤波器。如下图所示,我们需要做的是级联两个一阶RC 滤波器。

二阶RC滤波器的频率响应您可以根据您想要的截止频率设计一个一阶滤波器,并选择其中两个串联起来,形成一个二阶RC低通滤波器。这导致滤波器呈现出相似的整体频率响应,最大滚降为40 dB/decade,而不是20 dB/decade。然而,如果我们更仔细地观察响应,我们可以看到-3dB 频率的下降。二次RC 滤波器不能按预期工作,因为两个滤波步骤不是独立的。因此,不能简单地将两个滤波器连接在一起,将电路分析为一个一阶低通滤波器,叠加相同的一阶低通滤波器。它通过过滤。
此外,即使在两级之间插入了一个缓冲器,以便将第1 和第2 RC 用作独立滤波器,原始截止频率处的衰减也是6dB 而不是3dB。这是因为这两个命令独立工作。第一个滤波器在截止频率处有3dB 的衰减,第二个滤波器增加了另外3dB 的衰减,如下所示。二阶RC 低通滤波器的一个基本限制是设计人员无法通过调整滤波器的Q 因子来微调通过到停止的转换。该参数表示频率响应衰减了多少。晶体滤波器 腔体滤波器 大功率介质滤波器 介质波导滤波器当两个相同的RC 低通滤波器级联时,整体传递函数对应于二次响应,但Q 因子始终为0.5。当Q=0.5 时,滤波器处于过阻尼边缘,这会“降低”过渡区域的频率响应。二阶有源滤波器和二阶谐振滤波器没有这个限制,设计者可以控制Q因子来微调过渡域的频率响应。
总结所有电信号都包含所需和不想要的频率分量的混合。不需要的频率分量通常是由噪声和干扰引起的,在某些情况下会对系统性能产生负面影响。滤波器是对信号频谱的不同部分做出不同响应的电路。低通滤波器旨在通过低频分量并阻止高频分量。低通滤波器的截止频率表示滤波器从低衰减变为显着衰减的频率区域。 RC 低通滤波器的输出电压可以通过将电路视为由(频率无关)电阻和(频率相关)电抗组成的分压器来计算。幅度(纵轴上的dB)与对数频率(横轴上的赫兹)是研究滤波器理论行为的便捷有效的方法,而相位与对数频率的关系也可用于确定:应用于输入信号的相移量。二阶滤波器具有更陡峭的滚降,当信号不提供所需频率分量和不期望频率分量之间的宽带分离时,这种二阶响应很有用。通过制作两个相同的一阶RC 低通滤波器,然后将一个输出连接到另一个输入,可以创建一个二阶RC 低通滤波器,但预计总频率为-3dB。
[声明]文章版权归原作者所有,内容为作者个人观点,本站只提供参考并不构成任何投资及应用建议,转载目的在于传递更多信息,并不代表本站赞同其观点和对其真实性负责。如涉及作品内容、版权和其它问题,请在30日内与本网联系,我们将在第一时间删除内容!